[DP][JAVA] 2096번 내려가기

🔗문제 링크

https://www.acmicpc.net/problem/2096

2096번: 내려가기

 

문제 

N줄에 0 이상 9 이하의 숫자가 세 개씩 적혀 있다. 내려가기 게임을 하고 있는데,

이 게임은 첫 줄에서 시작해서 마지막 줄에서 끝나게 되는 놀이이다.

 

먼저 처음에 적혀 있는 세 개의 숫자 중에서 하나를 골라서 시작하게 된다. 그리고 다음 줄로 내려가는데,

다음 줄로 내려갈 때에는 다음과 같은 제약 조건이 있다.

바로 아래의 수로 넘어가거나, 아니면 바로 아래의 수와 붙어 있는 수로만 이동할 수 있다는 것이다.

이 제약 조건을 그림으로 나타내어 보면 다음과 같다.

 

 

별표는 현재 위치이고, 그 아랫 줄의 파란 동그라미는 원룡이가 다음 줄로 내려갈 수 있는 위치이며,

빨간 가위표는 원룡이가 내려갈 수 없는 위치가 된다.

숫자표가 주어져 있을 때, 얻을 수 있는 최대 점수, 최소 점수를 구하는 프로그램을 작성하시오.

점수는 원룡이가 위치한 곳의 수의 합이다.

 

입력

첫째 줄에 N(1 ≤ N ≤ 100,000)이 주어진다.

다음 N개의 줄에는 숫자가 세 개씩 주어진다. 숫자는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 중의 하나가 된다.

 

 

👩‍💻 문제코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

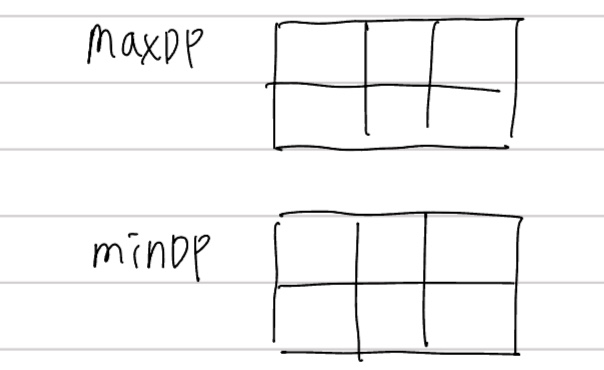
		//최대값 계산 위한 maxDP, 2개의 행, 3개의 열(숫자가 3개씩 주어짐)
        int[][] maxDP = new int[2][3];
        //최소값 계산 위한 minDP
        int[][] minDP = new int[2][3];

        for (int i = 0; i < N; i++) {
            String[] input = br.readLine().split(" ");

            int[] arr = new int[3];
            // 3번 반복하는 반복문
            for (int j = 0; j < 3; j++) {
                arr[j] = Integer.parseInt(input[j]);
            }

            maxDP[1][0] = Math.max(maxDP[0][0], maxDP[0][1]) + arr[0];
            maxDP[1][1] = Math.max(Math.max(maxDP[0][0], maxDP[0][1]), maxDP[0][2]) + arr[1];
            maxDP[1][2] = Math.max(maxDP[0][1], maxDP[0][2]) + arr[2];

            minDP[1][0] = Math.min(minDP[0][0], minDP[0][1]) + arr[0];
            minDP[1][1] = Math.min(Math.min(minDP[0][0], minDP[0][1]), minDP[0][2]) + arr[1];
            minDP[1][2] = Math.min(minDP[0][1], minDP[0][2]) + arr[2];

			//maxDP 배열의 두 번째 행 값을 첫 번째 행으로 복사합니다.
            System.arraycopy(maxDP[1], 0, maxDP[0], 0, 3);
            System.arraycopy(minDP[1], 0, minDP[0], 0, 3);
        }

        int maxResult = Math.max(Math.max(maxDP[0][0], maxDP[0][1]), maxDP[0][2]);
        int minResult = Math.min(Math.min(minDP[0][0], minDP[0][1]), minDP[0][2]);

        System.out.println(maxResult + " " + minResult);

        br.close();
    }
}

 

📌자세히 보기 

#DP를 사용하여 최댓값과 최솟값을 구하는 부분

maxDP[1][0] = Math.max(maxDP[0][0], maxDP[0][1]) + arr[0];
maxDP[1][1] = Math.max(Math.max(maxDP[0][0], maxDP[0][1]), maxDP[0][2]) + arr[1];
maxDP[1][2] = Math.max(maxDP[0][1], maxDP[0][2]) + arr[2];

minDP[1][0] = Math.min(minDP[0][0], minDP[0][1]) + arr[0];
minDP[1][1] = Math.min(Math.min(minDP[0][0], minDP[0][1]), minDP[0][2]) + arr[1];
minDP[1][2] = Math.min(minDP[0][1], minDP[0][2]) + arr[2];

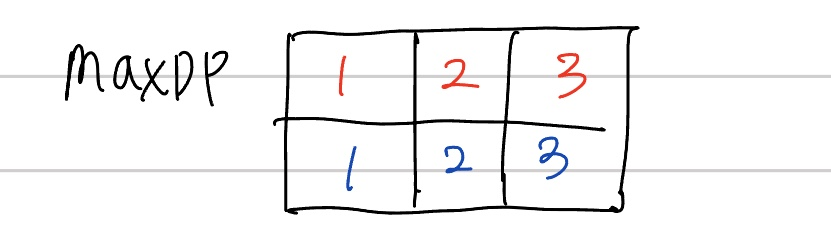
maxDP 배열은 크기가 2x3인 배열로, 이전 단계와 현재 단계의 최댓값을 저장함

maxDP[1][0]은 첫 번째 열에서의 최댓값을 계산합니다.

이전 단계의 첫 번째 열(maxDP[0][0])과 두 번째 열(maxDP[0][1]) 중 더 큰 값을 선택하고,

현재 단계의 값을 더해줍니다. (arr[0]은 입력 배열에서의 값입니다.)

 

maxDP[1][1]은 두 번째 열에서의 최댓값을 계산합니다.

이전 단계의 첫 번째 열(maxDP[0][0]), 두 번째 열(maxDP[0][1]), 그리고 세 번째 열(maxDP[0][2]) 중 가장 큰 값을 선택하고, 현재 단계의 값을 더해줍니다. (arr[1]은 입력 배열에서의 값입니다.)

 

maxDP[1][2]는 세 번째 열에서의 최댓값을 계산합니다.

이전 단계의 두 번째 열(maxDP[0][1])과 세 번째 열(maxDP[0][2]) 중 더 큰 값을 선택하고, 현재 단계의 값을 더해줍니다. (arr[2]은 입력 배열에서의 값입니다.)

 

이렇게 최댓값을 구하는 점화식을 이용하여 maxDP 배열을 갱신해나갑니다.

 

---

- 문제에서는 첫째줄의 입장에서 얘기했지만

코드를 작성할 때는 둘째줄에 입장에서 코드를 작성하면 된다. 

 

- 복사함

 

 

- 전체  

 

 

🚀 이건 몰랐네

maxDP[0][0] 에 값을 언제 넣었어?

: maxDP 배열은 크기가 2x3로 선언되었는데, 초기에는 모든 요소들이 0으로 초기화됩니다.

 

System.arraycopy 사용법! 

 System.arraycopy(sourceArray, sourcePos, destinationArray, destinationPos, length);

• sourceArray: 복사할 원본 배열입니다.
• sourcePos: 원본 배열에서 복사를 시작할 인덱스입니다.
• destinationArray: 복사한 데이터를 저장할 대상 배열입니다.
• destinationPos: 대상 배열에 복사한 데이터를 저장할 시작 인덱스입니다.
• length: 복사할 요소의 개수입니다.

System.arraycopy(maxDP[1], 0, maxDP[0], 0, 3);

System.arraycopy(minDP[1], 0, minDP[0], 0, 3);

 

 

 

 

 

 

 

 

 

 

 

취업과 이직을 위한 프로그래머스 코딩 테스트 문제 풀이 전략 : 자바 편

"이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다."